The A.CRE Method for Doing Cap Rate Math in Your Head

In this post, I’d like to share a method that, with a little practice, will enable you to quickly do cap rate math in your head; whether it’s quickly figuring out what the sale or purchase price would be of a property based on the NOI and cap rate or, inversely, figuring out what the NOI should be based on a purchase or sale price and the cap rate.
 
This is a step-by-step guide on how this method works that includes study flash cards along the way so that you can test your understanding. I hope you find this both enjoyable and useful. Please feel free to reach out with any feedback as you try it out.

Background to Developing this Method

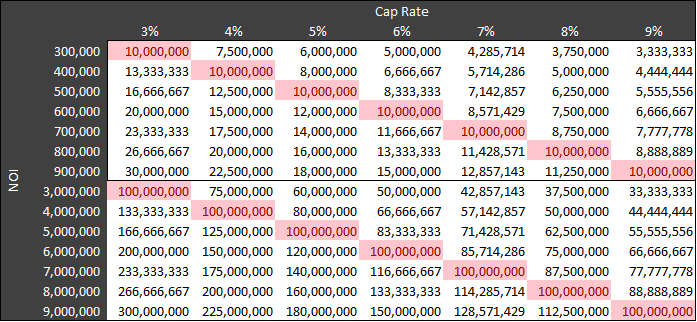
The first step towards developing this method was to create a few tables with various NOIs, cap rates, and their resulting values; and to look for patterns that might be universal. When I created the table below, the first thing that was immediately apparent was the following:

All NOI numbers that began with X and were divided by an X% cap rate equaled a power of 10. More specifically, the formula would be the following:

X * 10^y / (X/100) = 10^y+2

NOTE: DO NOT WASTE ANY TIME TRYING TO MEMORIZE THIS FORMULA!

For example, a $400k NOI with a 4% cap rate equals a $10MM purchase price and a $4MM NOI with a 4% cap rate equals $100MM.

Soon after, I had another important realization:

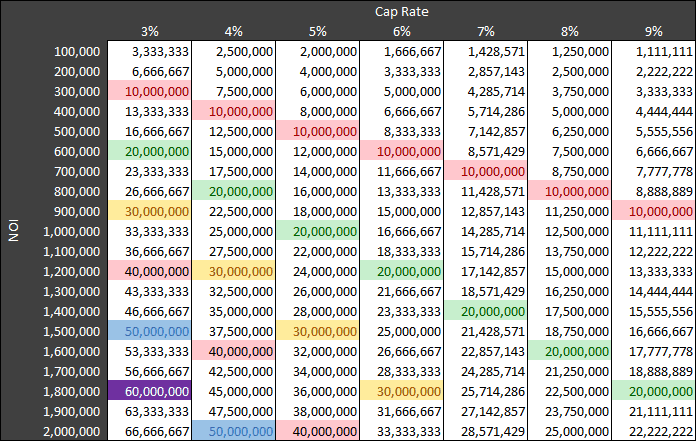
If a $400k NOI at a 4% cap rate was $10MM, then every additional $400k in NOI at a 4% cap rate would equal an additional $10MM in value. So an $800k NOI ($400k x 2) at the same 4% cap rate would result in a $20MM sale price ($10MM * 2), or a $1.2MM NOI (400k x 3) would be a $30MM sale price.

This table below highlights this rule for different cap rates:

While reading through the step-by-step guide below, keep the above in mind. By following the steps, working to memorize a series of fraction values as decimals, and some practice you should be able to derive rough property values based on cap rates quickly with nothing but a few seconds to think about it.

The A.CRE Method to Doing Cap Rate Math in Your Head

Step 1:

Take the cap rate you are using and move the decimal point to the right until the cap rate number becomes a value that is as close as possible to the value of the NOI. For example, if the NOI is $1,400,000 and your cap rate is 7%, or .07; then the value closest to the NOI based on moving the decimal point of the cap rate to the right would be 700,000. If you have an NOI of 3,000,000 and your cap rate is 4%, then the value closest to the NOI will be 4,000,000. The number derived from this first step will from hereon in be referred to as the Cap Rate Value Match (CRVM).

As with all the steps in the A.CRE method, this should be a fairly easy process.

Step 2:

The second step is to take the CRVM from Step 1 and divide it by the cap rate to get what we will refer to from hereon as the Power of Ten Number (PTN). To do this is actually very easy. The PTN will always be a power of ten that is two digits larger than the CRVM (see the tables above in the ‘Background to Developing This Method’ section above for verification) . If the CRVM is 650,000, then dividing 650,000 by the 6.5% cap rate will give you 10,000,000 (the power of 10 that is two digits larger than 650,000). If the CRVM is 5,000,000, then dividing by 5% will give you a PTN of 100,000,000. In our two examples from Step 1, the PTN of a 700,000 CRVM is 10,000,000 and the PTN of a 3,000,000 CRVM is 100,000,000.

Step 3:

In Step 3, we figure out how many times, if at all, the CRVM can wholly fit into the NOI and take that number and multiply it by the PTN.

Example

Using the example of a $1.4MM NOI and a 7% cap rate, the CRVM is $700,000 and and can fit into the $1,400,000 NOI 2 times. The PTN is 10,000,000 (700,000/.07 or the power of ten that is 2 digits larger than the CRVM). So, 2 (the amount of times the CRVM can fit completely into the NOI) times 10,000,000 (the PTN) equals $20MM and thus, that is what you would pay for a property with a year 1 NOI of $1.4MM and a cap rate of 7%.

There are still a couple more steps to learn and cap rates and NOI’s usually don’t fit so nicely together as they do in this example.

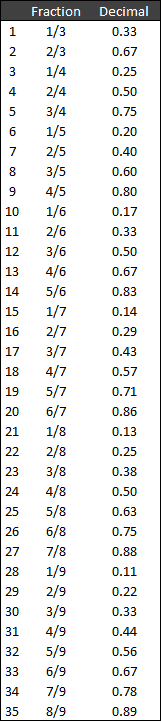
For Steps 4 & 5, practice and Memorize These Fractions

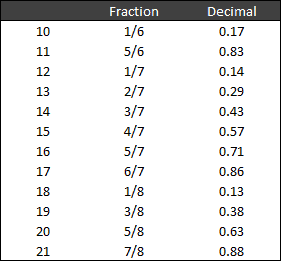
Very rarely will we find cap rates and NOI’s set up so nicely for us as in the previous section. The reality is that we get more difficult variables like 1,550,000 at a 6% cap rate. As a result, in order to get good at this method of deriving approximate values from cap rates in your head, it is critical to memorize the following 35 fractions and their decimal equivalents by heart:

Here are a few shortcuts, to help make this easier for you:

Fractions in this list that have the same decimal answer:

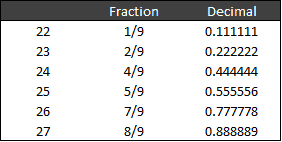
Fractions with 9 in the denominator always have the numerator in perpetuity as the result:

Most of us can divide by 5 relatively easy:

And that leaves us with 12 fractions that many of us will have to commit to memory:

Step 1-3 for a more challenging problem:

Before we get to Step 4, let’s first bring another example through Steps 1-3. Step 4 deals with valuing the part of the NOI that is left when you subtract the total CRVM’s that fit in the NOI from the NOI.

Example:

NOI: 1,650,000
Cap Rate: 6%

First, when doing mental math for cap rates, the idea is to get an approximate answer and it is not necessary to come up with the exact dollar, especially when having high level discussions. With this in mind, let’s round the NOI in this example to 1,700,000 and take it through Step 1. (If the NOI was in the hundred thousands, you should round to the nearest ten thousand)

Step 1: The CRVM here is $600,000 –

.06 – Cap rate
0.6
6
60
600
6,000
60,000
600,000 – closest in value to to the NOI = CRVM
6,000,000

Step 2: Divide the CRVM by the cap rate to get a PTN of $10,000,000 (600,000/.06)

Step 3: The CRVM fits in the NOI 2 times with $500,000 left over. Taking the amount of times the CRVM fits in the NOI (2) and multiplying it by $10,000,000 give us $20,000,000.

So, $1,200,000 (CRVM * 2) of the NOI at 6% is worth $20,000,000

Step 4:

In step 4, we work in fractions and it will be the only part of this method that might be a bit challenging unless you have mastered the fraction conversions above.

The remaining value of the NOI that has yet to be valued, which in this example is $500,000, will become the numerator and the CRVM, $600,000, will become the denominator. The remaining value of the NOI and the CRVM will usually be easy to reduce to a simple fraction. In this case, 500,000/600,000 = 5/6. And if we have memorized our fractions above, we know that 5/6 equals 0.83. Since we rounded up our NOI pre-step 1, we should round down our decimal number to the nearest tenth to compensate. In this case, we can round down to 0.8

Step 5:

Multiply the PTN by 0.8. So 10,000,000 * 0.8 = $8,000,000. Add that to the $20,000,000 from step 3 and we have a value of ≈ $28MM

The exact answer is $27.5MM and $28MM is only 1.8% above.

Wrap Up

That is all there is to it! As you get better with this, the goal is to just be on auto-pilot to the point where you are not thinking about the labels or steps and you just go through the process fluidly and automatically.  I hope the A.CRE Method for doing cap rate math in your head becomes a useful tool for you! Also, if any of our readers have any other tricks for doing cap rate math or any other back of the envelope math for real estate quickly in your head, I’d love to hear from you!

---

Frequently Asked Questions about the A.CRE Method for Doing Cap Rate Math in Your Head

---